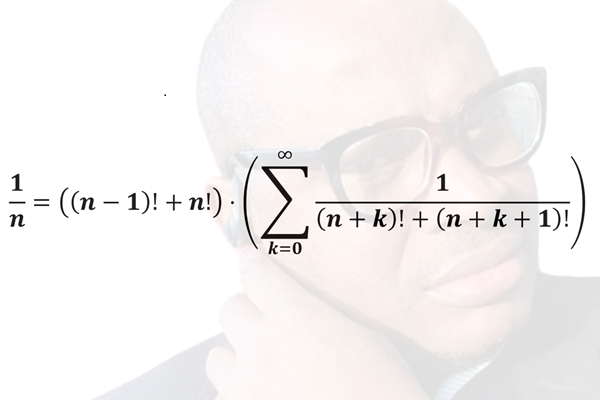
La formule inversée de Claude Kazadi est innovante et apporte plusieurs valeurs ajoutées par rapport aux formules traditionnelles existantes
Utilisant une combinaison de factorielles et de séries infinies, la formule inversée de Claude Kazadi est innovante et apporte plusieurs valeurs ajoutées par rapport aux formules traditionnelles existantes, telles que les séries de Taylor, de Maclaurin, les fractions continues ou les expressions harmoniques. Ces valeurs ajoutées sont analysées en termes de précision, convergence, applications pratiques et perspectives d'utilisation dans divers domaines (industrie, aéronautique, médecine, environnement, hydrocarbures, opérations militaires, balistique, informatique, etc.)
Cette formule permet l’optimisation des ressources dans les systèmes industriels (répartition proportionnelle, planification à long terme) , les applications en sciences économiques et sociales, la contribution aux modèles d'intelligence artificielle et de machine learning, la modélisation des rendements décroissants (Analyse des cycles de production, modélisation des contributions marginales, Optimisation des configurations multi-étapes), l’analyse des systèmes asymptotiques (Décroissance exponentielle des pertes et Simulation des performances), les algorithmes d'optimisation et d’apprentissage (Construction d’algorithmes d’apprentissage, optimisation des systèmes itératifs, réduction des coûts de calcul).
Cette même formule peut jouer un rôle concret et innovant dans le domaine médical
Dans le domaine aéronautique, cette formule apporte des solutions dans l’optimisation des performances et de la consommation énergétique, la maintenance prédictive, la simulation des performances en vol, l’optimisation des opérations aériennes, la conception et innovation technologique, le développement des algorithmes pour l’aviation, sans oublier l’optimisation des moteurs, la modélisation des pertes thermiques ou des rendements mécaniques des turbines en fonction de l’usure, a planification des cycles de maintenance des moteurs, la gestion du carburant, l’optimisation en temps réel de la consommation pour maximiser l’efficacité énergétique pendant le vol et la simulation des scénarios d’urgence.
Cette même formule peut jouer un rôle concret et innovant dans le domaine médical : la modélisation des processus biologiques, la planification et optimisation des traitements, l’analyse des données médicales, l’optimisation des opérations médicale, la recherche et développement médical, l’applications en intelligence artificielle médicale, le traitement du cancer (la modélisation de l’efficacité décroissante des cycles de chimiothérapie et optimisation des protocoles), la gestion des pandémies, la modélisation de la fatigue médicale dont l’optimisation des horaires des équipes médicales en fonction de la décroissance progressive de la productivité avec le temps.
À SUIVRE...



